الگوریتم فیبوناچی چیست؟

الگوریتم فیبوناچی، یکی از زیباترین الگوریتم‌ها در طبیعت و معروف‌ترین دنباله‌ها در دنیای ریاضیات است. این الگوریتم حتی در هنر هم کاربرد خود را دارد. در ادامه این مطلب با دنباله فیبوناچی، کاربرد و زیبایی‌های اسرارآمیز آن بیشتر آشنا خواهید شد؛ با ما همراه باشید.

فیبوناچی در ریاضیات یک دنباله عددی ادامه‌دار است. پرداختن به این دنباله اولین بار توسط لئوناردو فیبوناچی می‌دانند؛ آن هم در زمانی که قصد داشت تعداد جفت‌گیری یک زوج خرگوش را در یک سال حدس بزند؛ اما این اولین بار نبود که انسان‌ها به الگوریتم فیبوناچی برمی‌خوردند. پیش از لئوناردو، اولین‌بار در متن‌های سانسکریت از فیبوناچی در سیستم اعداد هندو_عربی استفاده شده بود. این متون قرن‌ها پیش از لئوناردو وجود داشته‌ است.

در واقع لئوناردو در سال 1202 در کتابی با نام «Liber Abaci» که برای محاسبه سود و زیان بازرگانان نوشته بود، از این دنباله استفاده کرد. مسئله خرگوش‌ها را هم در این همین کتاب مطرح کرد. در واقع می‌توان گفت دنیای غرب با این کتاب با مسئله فیبوناچی آشنا شد. دنباله فیبوناچی در ریاضی، با عدد صفر (0) و یک (1) آغاز می‌شود. در ادامه دو عدد قبلی با یکدیگر جمع شده و عدد بعدی دنباله را تشکیل میدهند. این دنباله به صورت زیر ادامه پیدا خواهد کرد:

…،۰،۱،۱،۲،۳،۵،۸،۱۳،۲۱،۳۴

کاربرد دنباله فیبوناچی بسیار زیاد است. پس از دنیای ریاضی، بیشترین جایی که با دنباله فیبوناچی بر می‌خوریم، طبیعت است. به صورتی که به الگوریتم فیبوناچی، راز مخفی طبیعت و قانون جهانی طبیعت می‌گویند. کهکشان‌ها، صدف دریایی، زنبورهای عسل و مولکول‌های دی‌ان‌ای همگی از این دنباله پیروی می‌کنند. فیبوناچی در دنیای هنر هم کاربرد دارد؛ یکی از بهترین ترکیب‌بندی‌ها برای عکاسی، ترکیب‌بندی بر اساس فیبوناچی است که مارپیچ طلایی هم نام دارد. موسیقی نیز از این دنباله بی‌بهره نمانده است. در آثار نقاشان بزرگ هم به دنباله فیبوناچی برمی‌خوریم که در ادامه بیشتر به آن‌ها می‌پردازیم.

انجام پروژه‌های ریاضی یا جبر خطی توسط بهترین متخصصان ایران

علت شهرت دنباله فیبوناچی

الگوریتم فیبوناچی یک دنباله از اعداد است. با وجود گستردگی طبیعت، این الگوریتم در انواع موجودات زنده، انسان‌ها، و طبیعت بی‌جان قابل مشاهده است؛ زیرا همه چیز در طبیعت از یک نظم خاصی پیروی می‌کند. دنیای ریاضیات هم یکی از علوم پایه است که کشف اسرار آن، کلید حل معمای موجود در طبیعت است. شاید در حال حاضر از نظم پنهان‌شده در پشت‌ بسیاری از چیزها آگاه نباشیم، اما با پیشرفت علم، کم‌کم این نظم آشکارتر می‌شود.

یکی از مواردی که در طبیعت بر روی نظمی خاص آفریده شده است، لاک حلزون است. لاک حلزون بر اساس زاویه فی در قسمت لاک حلزون ساخته شده؛ حتی شاخ‌وبرگ درختان هم به‌صورت تصادفی در رشد نمی‌کنند و جهت آن‌ها از یک الگوی خاص پیروی می‌کند. متخصصان این حوزه معتقدند که الگوی رشد شاخه‌های درختان، از نظمی شبیه الگوریتم فیبوناچی و نسبت طلایی پیروی می‌کند. به طور کلی شاخه‌های درختان با پیروی از این الگو، می‌توانند نور بیشتری از خورشید را جذب کنند. به دلیل همین زیبایی‌های موجود در طبیعت است که فیبوناچی و الگوهای نشئت‌گرفته از آن، مشهور شده‌اند.

مطلب پیشنهادی: پارادایم شیفت چیست؟

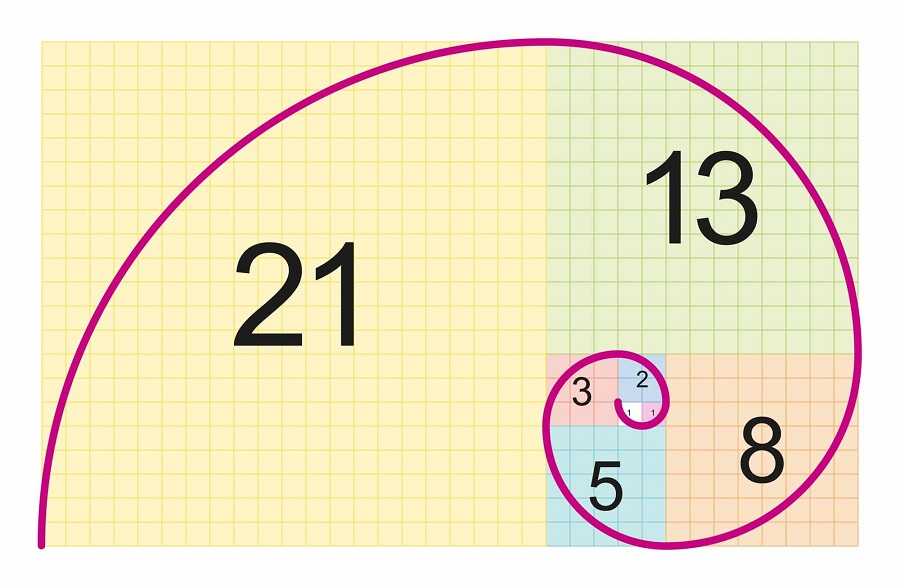
مارپیچ طلایی

الگوهای بسیاری از الگوریتم فیبوناچی نشئت گرفته‌اند. مارپیچ طلایی یکی از آن‌ها است. در اطراف این مارپیچ، مستطیل طلایی تشکیل می‌شود. این مارپیچ از یک‌چهارم دایره‎های متصل به یکدیگر تشکیل شده که این دایره‌ها درون مربع‌هایی قرار دارند. ابعاد مربع‌ها نیز از اعداد فیبوناچی پیروی می‌کنند. این مارپیچ برای ترکیب‌بندی عکاسی، کاربرد بسیاری دارد. در طبیعت نیز گل کلم، تخمه‌های آفتاب‌گردان و غیره بر اساس این مارپیچ درون یکدیگر قرار گرفته‌اند.

مطلب پیشنهادی: مهندسی فرایند چیست؟

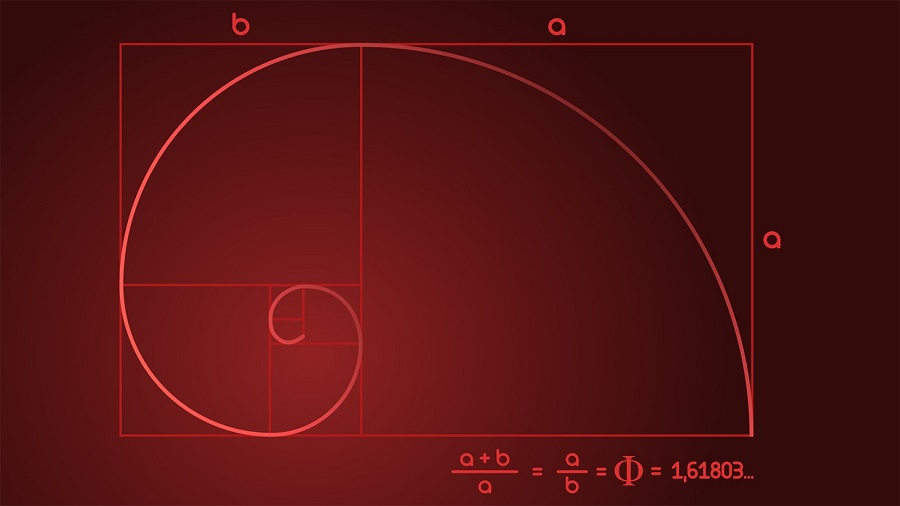
نسبت طلایی

از الگوهای دیگر نشئت‌گرفته از فیبوناچی، نسبت طلایی است. نسبت طلایی در واقع رابطه ریاضی بین دو عدد را نشان می‌دهد. زمانی میان دو عدد نسبت طلایی برقرار است که نسبت مجموع همان دو عدد (a+b) تقسیم بر عدد بزرگ‌تر (a) مساوی باشد با نسبت عدد بزرگ‌تر تقسیم بر عدد کوچک‌تر  (a/b). این نسبت تقریبا با عدد ۱٫۶۱۸ برابر است. در ارتباط با رابطه نسبت طلایی با الگوریتم فیبوناچی باید گفت که در دنباله فیبوناچی هرچه اعداد بزرگ‌تر می‌شوند، نسبت آن‌ها به ۱٫۶۱۸ نزدیک‌تر می‌شود.

مطلب پیشنهادی: رگرسیون لجستیک چیست؟

کاربرد فیبوناچی

فیبوناچی کاربردهای بسیاری در علوم مختلف دارد. از فیبوناچی در علم اقتصاد، بورس، انجام پروژه فیزیک، طبیعت، هنر، انجام پروژه معماری و غیره به‌وفور استفاده می‌کنند. در ادامه کاربردهای فیبوناچی در علوم مختلف را بیان می‌کنیم:

معماری

یکی از علومی که از این دنباله بهره می‌برد، معماری است. به عنوان مثال از نسبت طلایی در معماری هرم بزرگ جیزه در مصر استفاده شده است. به صورتی که با تقسیم محیط هرم جیزه بر دو برابر ارتفاع عمودی آن نسبت طلایی به دست می‌آید.

طبیعت

فیبوناچی، دنباله آن، مارپیچ طلایی و نسبت طلایی را می‌توان به راحتی در طبیعت مشاهده کرد؛ البته این صرفا به طبیعت بی‌جان ختم نمی‌شود. یکی از این موارد تعداد گلبرگ‌های گل‌ها است که همیشه از الگوریتم فیبوناچی پیروی می‌کنند. به عنوان مثال گل کاسنی با  ۲۱ گلبرگ، گل دیزی با ۳۴ گلبرگ و گل‌هایی با ۵۵ یا ۸۹ گلبرگ را در طبیعت داریم. همان‌طور که پیش از این هم گفتیم نحوه قرار گرفتن تخمه‌های گل آفتاب‌گردان در مرکز آن هم از مارپیچ طلایی پیروی می‌کند.

مارپیچ طلایی را می‌توان در رشد تنه درخت هم مشاهده کرد. شاخه‌های درختان نیز از نسبت طلایی پیروی می‌کنند. به این صورت که تنه درخت ابتدا به دو قسمت تقسیم می‌شود و هر یک از آن دو قسمت خود به چند شاخه تبدیل می‌شوند. در هنگامه شب یا در کویر کهکشان‌ها قابل مشاهده هستند. در آن زمان به راحتی می‌توان پیروی کهکشان‌ها را از مارپیچ طلایی دید. از جمله این کهکشان‌ها، کهکشان راه شیری، آندرومدا و M81  هستند.

اگر تعداد زنبورهای ماده موجود در یک کندو را بر تعداد نرها تقسیم کنید، عدد نسبت طلایی یعنی ۱٫۶۱۸ یا نزدیک به آن به دست می‌آید؛ زیرا ماده‌ها همیشه بیشتر از نرها هستند.

بدن انسان

از موارد دیگر در استفاده از الگوریتم فیبوناچی، بدن انسان است. به عنوان ملموس‌ترین مثال، می‌توان از فاصله دهان و بینی با چشم‌ها تا پایین چانه نام برد که هرکدام از این قسمت‌ها، از نسبت طلایی پیروی می‌کنند. به صورت کلی قاعده‌ای وجود دارد که می‌گوید هرچه تناسب اندام فرد به عدد نسبت طلایی نزدیک‌تر باشد، آن فرد از به معیارهای زیبایی نزدیک‌تر است. اگر پهنای دندان‌های یک فرد نیز از نسبت طلایی پیروی کند یا به آن عدد نزدیک باشد، لبخند آن فرد زیباتر است. در این نسبت، باید دو دندان‌ جلو به اندازه ۱٫۶۱۸(نسبت طلایی) پهن‌تر از دندان‌های کناری باشند. دندان‌های کنار نیز که به نسبت ۱٫۶۱۸ از دندان‌های نیش پهن‌تر باشند.

 هنر

الگوریتم فیبوناچی را می‌توان در آثار هنری هنرمندانی مانند داوینچی، و موتزارت مشاهده کرد. تابلو مونالیزا داوینچی از مارپیچ طلایی الهام گرفته است. دنباله‌ فیبوناچی را در آثار موسیقی غربی و گام‌های موسیقی هم می‌توان مشاهده کرد که با استفاده از آن آثار خارق‌العاده‌ای شکل گرفته است.

موتزارت هم بسیاری از آثار خود را به مانند سونات‌های پیانو، بر اساس نسبت طلایی ساخته است. متخصصین حوزه موسیقی همچنین اعتقاد دارند بتهوون، بلا بارتوک، کلاد دبوسی، فرانتس شوبرت، باخ و اریک ساتی هم از این دنباله برای نوشتن سونات‌های خود استفاده کرده‌اند.

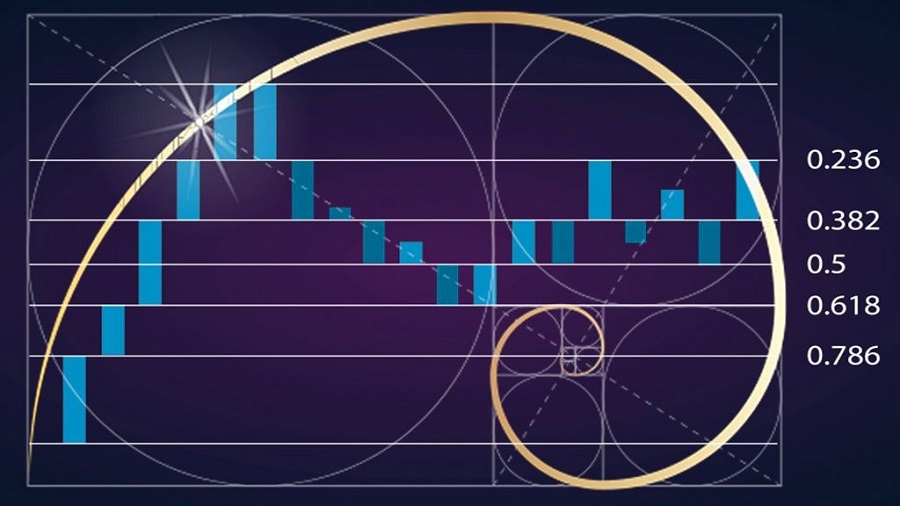
بورس

از اعداد فیبوناچی در بورس و بازار ارز و فارکس هم برای ورود به بازار و پیش‌بینی قیمت استفاده می‌شود. متخصصان در این زمینه اعتقاد دارند به کمک الگوریتم فیبوناچی، می‌توان رفتار بازار را با درصد خطای بسیار کمی (در حدود 30 دردصد خطا) پیش‌بینی کرد. برای تحلیل تکنیکال نیز، ابزارهایی بر اساس نسبت‌های فیبوناچی ایجاد شده‌اند که به کمک افراد می‌ایند. این ابزرارها شامل:

• فیبوناچی اصلاحی: از مهم‌ترین ابزارهای فیبوناچی، ابزار فیبوناچی اصلاحی است. با استفاده از این ابزار می‌توان درصدهای احتمالی را برای پایان یک حرکت اصلاحی تخمین زد و نقاط ورود مناسبی را به دست آورد.
• فیبوناچی خارجی: این ابزار برای پیش‌بینی سطح قیمت‌های بیش از ۱۰۰ درصد به کار می‌آید. به این ‌صورت که اگر سهمی از سقف قبلی خود عبور کند، برای شناسایی سطوح مقاومتی جدید سهم پس از عبور از سقف قبلی، از این ابزار می‌توان استفاده کرد.
• فیبوناچی انبساطی: از این ابزار الگوریتم فیبوناچی می‌توان برای پیش‌بینی سطوح قیمت در آینده و تشخیص سطوح مقاوم استفاده کرد.
• فیبوناچی پروژكشن: تریدرها می‌توانند از این ابزار برای تنظیم حد سود خود استفاده ‌کنند.
• فیبوناچی کمان‌‌ها: این ابزار نقاط بازگشت قیمت را بر مبنای صعودی یا نزولی بودن روند، مشخص می‌کنند.
• فیبوناچی باد‌بزن: این ابزار برای تحلیل ترازهای اصلاحی و پیش‌بینی بازگشت قیمت به کار می‌رود.
• فیبوناچی کانال: این ابزار، ساده‌ترین نوع فیبوناچی است. از آن برای تحلیل نمودارهای قیمتی که در یک کانال در حرکت هستند استفاده می‌شود. در زمان شکست کانال هم می‌توان نقاط حمایت و مقاومت بر سر راه قیمت را بر اساس ابزار خطوط کانال شناسایی کرد.

مطلب پیشنهادی: الگوریتم میگو در متلب

جمع‌بندی

الگوریتم فیبوناچی یا همان دنباله فیبوناچی در ریاضیات یک دنباله اعداد است که بر اساس آن اعداد طبق یک الگو به صورت دنباله در کنار یکدیگر قرار می‌گیرند. این الگوریتم کاربردهای بسیاری در معماری، موسیقی، هنر، بورس و بازارهای مالی دارد؛ به صورتی که برای پیش‌بینی قیمت کالا، بازار و مشخص کردن حد سود هم قابلیت استفاده دارد. مجسمه‌سازها، نقاش‌ها، موسیقیدان‌ها هم گاهی به طور ناخودآگاه از این تناسب برای خلق یک مجسمه، تابلوی نقاشی و موسیقی بهره می‌برند. نسبت طلایی و مارپیچ طلایی نیز از فیبوناچی الهام گرفته شده است که به‌وفور در طبعت مانند لاک حلزون، چینش تخمه‌های گل آفتاب‌گردان و رشد شاخه‌های درختان قابل مشاهده هستند.