پیمایش درخت در ساختمان داده

پیمایش درخت یکی از مفاهیم بنیادی در علم ساختمان داده‌ها است. درخت‌ها ساختارهای داده‌ای سلسله مراتبی هستند که برای نمایش روابط سلسله مراتبی بین داده‌ها استفاده می‌شوند. پیمایش درخت به معنای بازدید از تمام گره‌های یک درخت به ترتیبی مشخص است. این عمل در بسیاری از الگوریتم‌ها و کاربردهای مختلف از جمله مرتب‌سازی، جستجو، ساختارهای داده‌ای پیچیده‌تر و حتی در زمینه‌های هوش مصنوعی به کار می‌رود. در این مقاله، به بررسی انواع مختلف و کاربردهای آن‌ها خواهیم پرداخت.

مفاهیم پایه

قبل از اینکه به انواع پیمایش درخت بپردازیم، لازم است با برخی از مفاهیم پایه در مورد درخت‌ها آشنا شویم:

• گره: (Node) هر عنصر در یک درخت یک گره نامیده می‌شود.
• ریشه : (Root) گره بالایی‌ترین سطح در درخت است که هیچ والدینی ندارد.
• فرزند : (Child) گره‌هایی که مستقیماً زیر یک گره قرار دارند، فرزندان آن گره نامیده می‌شوند.
• والد : (Parent) گره‌ای که مستقیماً بالای یک گره قرار دارد، والد آن گره نامیده می‌شود.
• برگ : (Leaf) گره‌هایی که هیچ فرزندی ندارند، برگ نامیده می‌شوند.
• درخت دودویی : (Binary Tree) درختی است که هر گره حداکثر دو فرزند دارد.

انجام پروژه‌ هوش مصنوعی توسط متخصصان حرفه‌ای

انواع پیمایش درخت

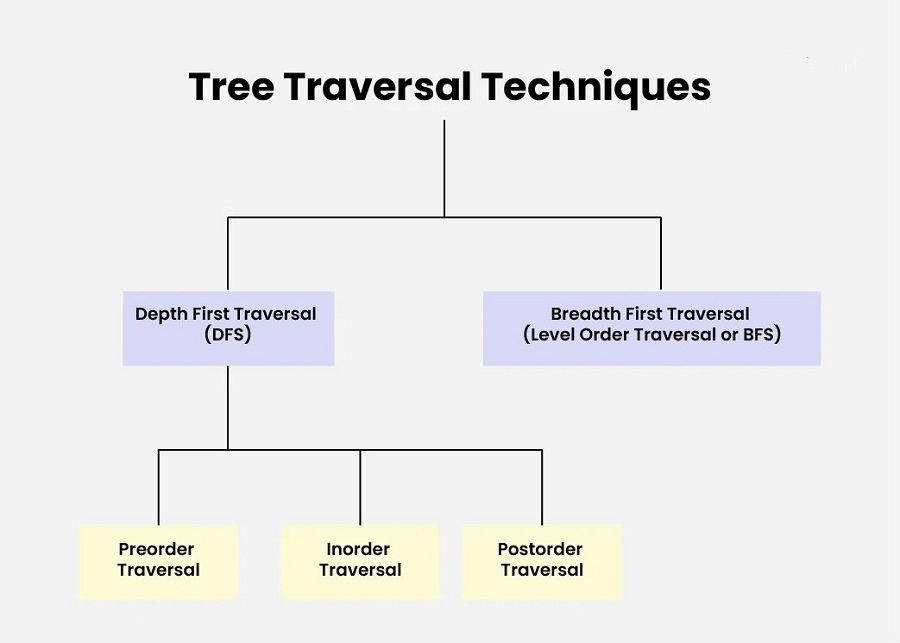
پیمایش درخت را می‌توان به روش‌های مختلفی انجام داد. هر روش، ترتیب بازدید از گره‌ها را به گونه‌ای متفاوت مشخص می‌کند. رایج‌ترین روش‌های پیمایش درخت عبارتند از:

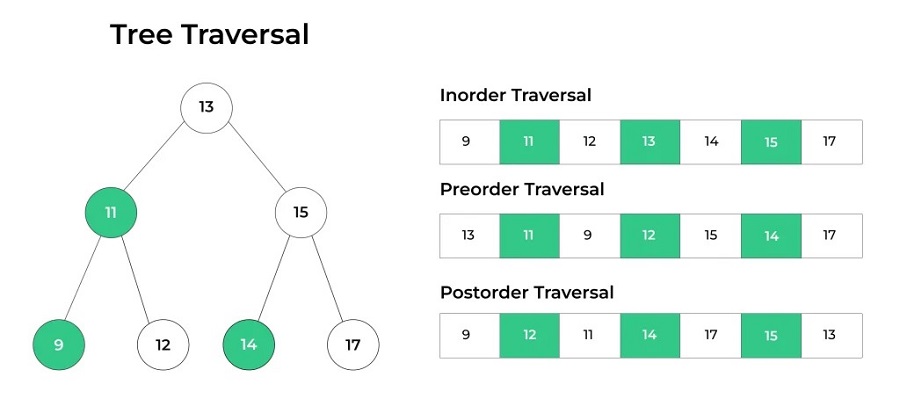
۱. پیمایش پیش‌سفری (Pre-order Traversal)

در این روش، ابتدا ریشه، سپس زیر درخت چپ و در نهایت زیر درخت راست پیمایش می‌شود. این روش برای ایجاد یک کپی از درخت یا برای تبدیل درخت به یک عبارت پیش‌وند در عبارات ریاضی مفید است.

۲. پیمایش میان‌سفری (In-order Traversal)

در این روش، ابتدا زیر درخت چپ، سپس ریشه و در نهایت زیر درخت راست پیمایش می‌شود. این روش برای مرتب‌سازی داده‌ها در یک درخت جستجوی دودویی مفید است.

۳. پیمایش پس‌سفری (Post-order Traversal)

در این روش، ابتدا زیر درخت چپ، سپس زیر درخت راست و در نهایت ریشه پیمایش می‌شود. این روش برای آزادسازی حافظه در یک درخت یا برای ایجاد یک عبارت پس‌وند در عبارات ریاضی مفید است.

۴. پیمایش سطحی (Level-order Traversal)

در این روش، گره‌ها بر اساس سطح خود پیمایش می‌شوند. ابتدا ریشه، سپس تمام گره‌های سطح دوم، سپس تمام گره‌های سطح سوم و به همین ترتیب تا رسیدن به آخرین سطح پیمایش می‌شوند. این روش برای پیاده‌سازی الگوریتم‌های جستجوی عرضی در گراف‌ها مفید است.

پیاده‌سازی پیمایش درخت

پیمایش درخت معمولاً به صورت بازگشتی پیاده‌سازی می‌شود. در پیاده‌سازی بازگشتی، یک تابع برای پیمایش یک گره تعریف می‌شود و این تابع برای فرزندان آن گره به صورت بازگشتی فراخوانی می‌شود. همچنین می‌توان پیمایش درخت را به صورت غیربازگشتی با استفاده از یک پشته پیاده‌سازی کرد.

مطلب پیشنهادی: تابع sum در پایتون چیست؟

کاربردهای پیمایش درخت

پیمایش درخت در بسیاری از کاربردهای مختلف مورد استفاده قرار می‌گیرد. برخی از این کاربردها عبارتند از:

• مرتب‌سازی: درخت‌های جستجوی دودویی برای مرتب‌سازی داده‌ها به کار می‌روند.
• جستجو: درخت‌های جستجو برای جستجوی یک عنصر خاص در یک مجموعه داده به کار می‌روند.
• ساختارهای داده‌ای پیچیده‌تر: درخت‌ها به عنوان پایه برای ساختارهای داده‌ای پیچیده‌تری مانند درخت‌های B، درخت‌های AVL و درخت‌های سرخ-سیاه استفاده می‌شوند.
• هوش مصنوعی: درخت‌های تصمیم‌گیری برای مدل‌سازی تصمیم‌گیری در سیستم‌های هوشمند استفاده می‌شوند.
• فشرده‌سازی داده‌ها: درخت‌های هافمن برای فشرده‌سازی داده‌ها به کار می‌روند.

مطلب پیشنهادی: درخت تصمیم چیست؟

تحلیل پیچیدگی در پیمایش درخت

تاکنون به بررسی انواع مختلف پیمایش درخت و کاربردهای آن‌ها پرداختیم. اما یک سوال مهم باقی می‌ماند: چقدر طول می‌کشد تا یک درخت پیمایش شود؟ برای پاسخ به این سوال، نیاز به تحلیل پیچیدگی الگوریتم پیمایش داریم. تحلیل پیچیدگی به ما کمک می‌کند تا کارایی الگوریتم را بر اساس اندازه ورودی (در این مورد، تعداد گره‌های درخت) ارزیابی کنیم.

مطلب پیشنهادی: الگوریتم علی بابا و چهل دزد چیست؟

پیچیدگی زمانی پیمایش درخت

پیچیدگی زمانی پیمایش درخت به نوع درخت، نوع پیمایش و نحوه پیاده‌سازی آن بستگی دارد. اما به طور کلی، می‌توان گفت که در اکثر موارد، پیچیدگی زمانی پیمایش درخت با تعداد گره‌های درخت متناسب است. به عبارت دیگر، اگر تعداد گره‌های درخت دو برابر شود، زمان اجرای الگوریتم پیمایش نیز تقریباً دو برابر می‌شود.

مطلب پیشنهادی: الگوریتم میگو در متلب

چرا پیچیدگی زمانی پیمایش درخت معمولاً O(n) است؟

• هر گره یک بار بازدید می‌شود: در تمام روش‌های پیمایش، هر گره دقیقاً یک بار بازدید می‌شود.
• عملیات ثابت در هر گره: در هر گره، عملیات ثابتی مانند دسترسی به فرزند چپ، فرزند راست یا مقدار گره انجام می‌شود.

توجه: O(n) نشان‌دهنده‌ی مرتبه‌ی زمانی الگوریتم است و به معنای آن است که زمان اجرای الگوریتم با رشد خطی تعداد گره‌ها افزایش می‌یابد.

عوامل موثر بر پیچیدگی زمانی

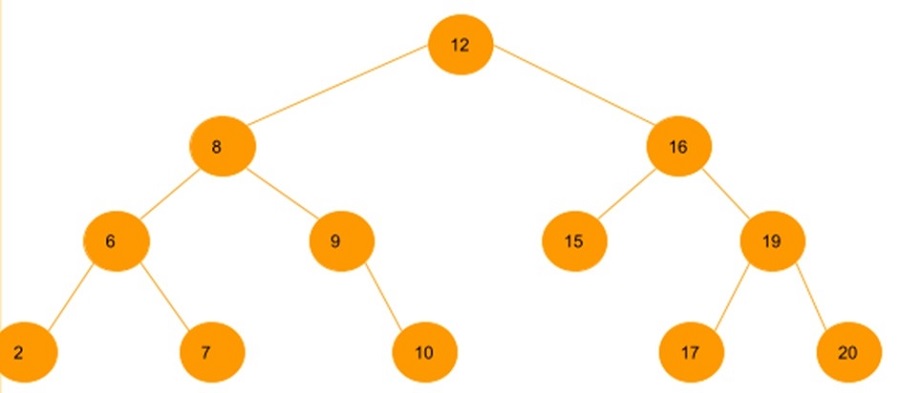
علاوه بر تعداد گره‌ها، عوامل دیگری نیز بر پیچیدگی زمانی پیمایش درخت تاثیرگذار هستند:

• نوع درخت: درخت‌های مختلف مانند درخت‌های دودویی کامل، درخت‌های دودویی جستجو و درخت‌های چندراهه، ساختارهای متفاوتی دارند که می‌تواند بر پیچیدگی زمانی پیمایش تاثیر بگذارد.
• نوع پیمایش: روش‌های مختلف پیمایش (پیش‌سفری، میان‌سفری، پس‌سفری، سطحی) می‌توانند پیچیدگی زمانی متفاوتی داشته باشند.
• نحوه پیاده‌سازی: پیاده‌سازی بازگشتی یا غیربازگشتی، استفاده از ساختارهای داده‌ای کمکی مانند پشته و صف، و بهینه‌سازی‌های مختلف می‌توانند بر پیچیدگی زمانی تاثیر بگذارند.

مثال: پیچیدگی زمانی پیمایش پیش‌سفری در یک درخت دودویی کامل

در یک درخت دودویی کامل، هر سطح درخت دارای حداکثر تعداد گره‌های ممکن است. در این حالت، پیچیدگی زمانی پیمایش پیش‌سفری دقیقاً برابر با تعداد گره‌های درخت خواهد بود.

مطلب پیشنهادی: تشخیص چهره با متلب

ابزارها و کتابخانه‌های محبوب برای پیاده‌سازی پیمایش درخت

در بخش‌های قبلی به مفاهیم پایه پیمایش درخت، انواع مختلف آن و کاربردهایش پرداختیم. حال به سراغ ابزارها و فریم ورک هایی می‌رویم که به برنامه‌نویسان کمک می‌کنند تا پیاده‌سازی پیمایش درخت را آسان‌تر و کارآمدتر کنند. این ابزارها و کتابخانه‌ها اغلب شامل کلاس‌ ها، توابع و ساختارهای داده‌ای از پیش تعریف شده‌ای هستند که برای کار با درخت‌ها بهینه شده‌اند.

زبان‌های برنامه‌نویسی و کتابخانه‌های استاندارد

اکثر زبان‌های برنامه‌نویسی مدرن، کتابخانه‌های استانداردی را برای کار با ساختارهای داده‌ای ارائه می‌دهند. این کتابخانه‌ها معمولاً شامل کلاس‌ها یا توابعی برای نمایش درخت‌ها و انجام عملیات پیمایش بر روی آن‌ها هستند. برخی از این زبان‌ها و کتابخانه‌های استاندارد عبارتند از:

•  C++: کتابخانه استاندارد C++ شامل کلاس‌های template برای نمایش درخت‌های دودویی و چندتایی است. همچنین، الگوریتم‌های پیمایش مختلف مانند   std::pre_order  , std::in_ order ,  و  std::post_ order در این کتابخانه موجود است.
• Java: کتابخانه Collections در جاوا کلاس ‌هایی مانند  TreeMap و  TreeSet را برای نمایش درخت‌های جستجوی دودویی ارائه می‌دهد. همچنین، می‌توان از رابط‌های  Iterator و   Iterable  برای پیمایش این درخت‌ها استفاده کرد.
•  Python: کتابخانه استاندارد پایتون شامل ماژول treelib است که برای کار با درخت‌ها طراحی شده است. همچنین، می‌توان از لیست‌ها و دیکشنری‌ها برای پیاده‌سازی درخت‌ها به صورت دستی استفاده کرد.

مطلب پیشنهادی: برنامه نویسی شی گرا چیست؟

کتابخانه‌های تخصصی

علاوه بر کتابخانه‌های استاندارد، کتابخانه‌های تخصصی دیگری نیز برای کار با درخت‌ها وجود دارند که امکانات پیشرفته‌تری را ارائه می‌دهند. برخی از این کتابخانه‌ها عبارتند از:

• Boost Graph Library (BGL)   : یک کتابخانه C++ قدرتمند برای کار با گراف‌ها و درخت‌ها است. BGL الگوریتم‌های مختلفی برای پیمایش درخت‌ها، جستجو در درخت‌ها و عملیات دیگر بر روی درخت‌ها ارائه می‌دهد.
•  Guava:یک کتابخانه جاوا است که مجموعه گسترده‌ای از ابزارهای مفید برای برنامه‌نویسی را ارائه می‌دهد. Guava کلاس‌های مختلفی برای نمایش درخت‌ها و انجام عملیات پیمایش بر روی آن‌ها دارد.
• NetworkX :  یک کتابخانه پایتون برای ایجاد و مطالعه گراف‌ها و شبکه‌ها است.  NetworkX می‌تواند برای نمایش درخت‌ها و انجام عملیات پیمایش بر روی آن‌ها استفاده شود.

انتخاب ابزار مناسب

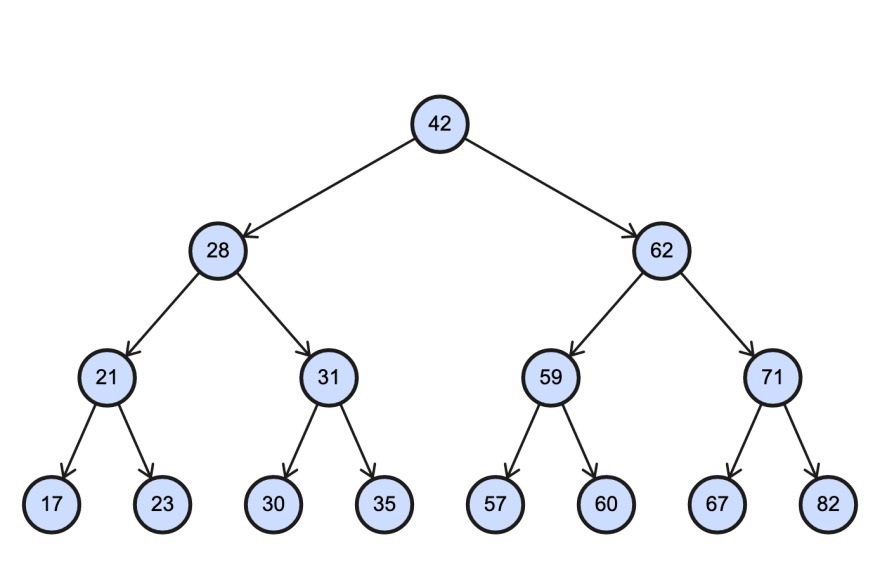
انتخاب ابزار مناسب برای پیاده‌سازی پیمایش درخت به عوامل مختلفی بستگی دارد، از جمله:

• زبان برنامه‌نویسی: زبانی که برای پروژه خود انتخاب کرده‌اید.
• پیچیدگی درخت: نوع درخت (دودویی، چندتایی، AVL، سرخ-سیاه و …) و اندازه آن.
• عملیات مورد نیاز: علاوه بر پیمایش، چه عملیات دیگری بر روی درخت نیاز دارید (جستجو، درج، حذف و …)؟
• کارایی: چه میزان کارایی برای شما اهمیت دارد؟
• سادگی استفاده: آیا می‌خواهید از یک کتابخانه آماده استفاده کنید یا درخت را به صورت دستی پیاده‌سازی کنید؟

مطلب پیشنهادی: دیباگ چیست؟

مزایای استفاده از کتابخانه‌ها

• کاهش زمان توسعه: کتابخانه‌ها کدهای از پیش نوشته شده و تست شده‌ای را در اختیار شما قرار می‌دهند.
• افزایش قابلیت اطمینان: کتابخانه‌ها معمولاً توسط توسعه‌دهندگان باتجربه نوشته شده‌اند و از نظر خطاهای برنامه‌نویسی ایمن‌تر هستند.
• امکانات پیشرفته: بسیاری از کتابخانه‌ها امکانات پیشرفته‌ای مانند بهینه‌سازی، موازی‌سازی و ویژوالایزیشن را ارائه می‌دهند.

استفاده از ابزارها و کتابخانه‌های مناسب برای پیاده‌سازی پیمایش درخت می‌تواند به شما کمک کند تا کدهای با کیفیت‌تر، کارآمدتر و قابل نگهداری‌تری بنویسید. با انتخاب ابزار مناسب، می‌توانید به طور موثر و کارآمد با درخت‌ها کار کنید و مشکلات پیچیده‌تری را حل کنید.

نتیجه‌گیری

در این پژوهش، به دنیای پیچیده و جذاب درخت‌ها در علم ساختمان داده‌ها قدم گذاشتیم. از مفاهیم پایه مانند گره، ریشه، برگ و انواع درخت‌ها شروع کردیم و به تدریج به دنیای پیمایش درخت‌ها وارد شدیم. پیمایشی که به ما امکان می‌دهد تا به صورت سیستماتیک و منظم از تمام گره‌های یک درخت بازدید کنیم.

انواع مختلف پیمایش، هر کدام با ویژگی‌ها و کاربردهای خاص خود، به ما ابزارهای قدرتمندی برای تحلیل و دستکاری درخت‌ها ارائه می‌دهند. از پیمایش پیش‌سفری که برای ایجاد یک کپی از درخت استفاده می‌شود تا پیمایش سطحی که برای پیاده‌سازی الگوریتم‌های جستجوی عرضی کاربرد دارد، هر کدام نقش مهمی در حل مسائل مختلف ایفا می‌کنند.

اما پیمایش درخت تنها به تئوری محدود نمی‌شود. در دنیای واقعی، ابزارها و کتابخانه‌های بسیاری وجود دارند که پیاده‌سازی پیمایش درخت را آسان‌تر و کارآمدتر می‌کنند. این ابزارها به برنامه‌نویسان اجازه می‌دهند تا با صرف زمان و انرژی کمتر، به نتایج دلخواه خود دست یابند.

در نهایت، می‌توان گفت که پیمایش درخت یکی از مفاهیم اساسی در علم ساختمان داده‌ها است و درک عمیق آن برای هر برنامه‌نویسی که با ساختارهای داده‌ای کار می‌کند ضروری است. با تسلط بر مفاهیم پیمایش درخت، می‌توانیم الگوریتم‌های کارآمدتری را طراحی کرده و مسائل پیچیده‌تری را حل کنیم.