توزیع نرمال چیست؟ خواص، کاربردها و فرمول

توزیع نرمال یکی از مهم‌ترین و پرکاربردترین توزیع‌های آماری به شمار می‌آید. این توزیع به دلیل شکل خاص و ویژگی‌های منحصر به فردش، در بسیاری از زمینه‌ها از جمله علوم اجتماعی، مهندسی، اقتصاد و زیست‌شناسی کاربرد دارد. در این مقاله، به بررسی موضوعاتی از قبیل ویژگی‌های توزیع نرمال و نحوه استفاده از توزیع نرمال در امور مالی، خواهیم پرداخت.

توزیع نرمال چیست؟

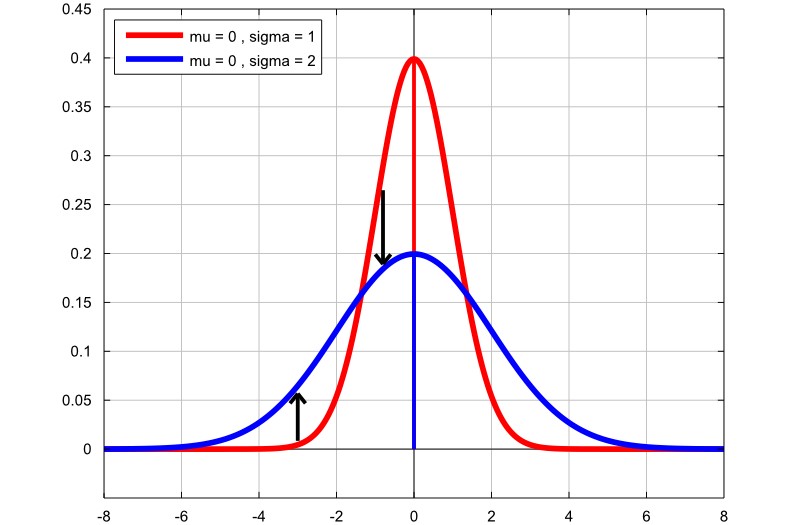
توزیع نرمال، یک توزیع پیوسته است که در آن مقادیر متغیر تصادفی به‌صورت متقارن حول یک مقدار میانگین توزیع می‌شوند. این توزیع به شکل یک منحنی زنگی (bell-shaped curve) ترسیم می‌شود که ویژگی‌های خاصی دارد. منحنی توزیع نرمال دارای دو پارامتر کلیدی است: میانگین (μ) و انحراف معیار (σ). توزیع نرمال در تحلیل‌های آماری و آزمون‌های فرضیه به طور گسترده‌ای مورداستفاده قرار می‌گیرد. این توزیع در زمینه‌های مختلف به‌عنوان یک مدل پایه شناخته می‌شود و به پژوهشگران کمک می‌کند تا رفتار داده‌ها را بهتر درک نمایند.

انجام پروژه آمار و احتمالات با بهترین هزینه توسط متخصصان حرفه‌ای

مفهوم توزیع نرمال

در توزیع نرمال، مقادیر حول یک مقدار مرکزی به نام میانگین متمرکز می‌شوند. این منحنی به‌صورت متقارن شکل‌گرفته و نشان‌دهنده این است که نیمی از مقادیر بالاتر و نیمی دیگر پایین‌تر از میانگین قرار دارند. از دیگر ویژگی‌های این توزیع، می‌توان به انحراف معیار اشاره نمود که نشان‌دهنده میزان پراکندگی داده‌ها نسبت به میانگین است. انحراف معیار تعیین می‌کند که منحنی چقدر پهن یا باریک باشد.

مطلب پیشنهادی: اوراق قرضه چیست؟

نمونه‌های اساسی توزیع نرمال: قد و وزن

توزیع نرمال یا توزیع گاوسی یکی از توزیع‌های آماری مهم است که در بسیاری از پدیده‌های طبیعی مشاهده می‌شود. در ادامه به چند نمونه اساسی از متغیرهایی که معمولاً توزیع نرمال دارند، اشاره می‌کنیم:

قد: قد افراد در یک جمعیت معمولاً توزیع نرمال دارد. به‌عنوان‌مثال، قد مردان و زنان در یک کشور مشخص می‌تواند به طور میانگین در یک محدوده خاص قرار گیرد و با افزایش یا کاهش قد، تعداد افراد نیز به طور متناسب تغییر کند.

وزن: وزن افراد نیز یکی دیگر از نمونه‌های توزیع نرمال است. وزن افراد در یک جمعیت معمولاً حول یک میانگین مشخص قرار دارد و به‌صورت سمتی (چپ یا راست) نسبت به این میانگین توزیع می‌شود.

پیشنهاد نویسنده: رگرسیون خطی چیست؟

ویژگی های توزیع نرمال

توزیع نرمال ویژگی‌های خاصی دارد که آن را از سایر توزیع‌ها متمایز می‌کند. برخی از مهم‌ترین ویژگی‌های توزیع نرمال عبارت‌اند از: قانون تجربی، چولگی در توزیع نرمال و کشیدگی در توزیع نرمال.

قانون تجربی

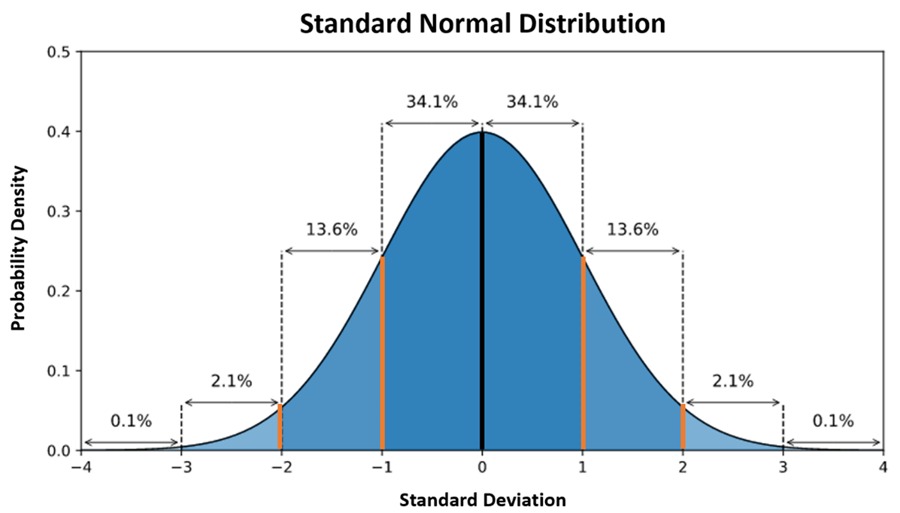
قانون تجربی در توزیع نرمال که به‌عنوان “قانون 68-95-99.7” نیز شناخته می‌شود، نشان‌دهنده توزیع فراوانی داده‌ها در یک توزیع نرمال است. این قانون به ما می‌گوید که چگونه داده‌ها در اطراف میانگین توزیع می‌شوند.

1. حدود 68% از داده‌ها در یک انحراف معیار (σ) از میانگین (µ) قرار دارند. به عبارت دیگر، اگر مقدار میانگین را در نظر بگیریم، 68% از مقادیر در بازه (µ – σ) تا (µ + σ) قرار خواهند گرفت.
2. حدود 95% از داده‌ها در دو انحراف معیار از میانگین قرار دارند. یعنی 95% از مقادیر در بازه (µ – 2σ) تا (µ + 2σ) قرار خواهند گرفت.
3. حدود 99.7% از داده‌ها در سه انحراف معیار از میانگین قرار دارند. به این معنا که 99.7% از مقادیر در بازه (µ – 3σ) تا (µ + 3σ) قرار خواهند گرفت.

چولگی در توزیع نرمال

چولگی در توزیع نرمال به معنای عدم تقارن و انحراف از توزیع ایده‌آل نرمال است. در توزیع نرمال، منحنی به‌صورت متقارن و زنگی شکل می‌باشد و میانگین، میانه و نما در یک نقطه قرار دارند.

کشیدگی در توزیع نرمال

کشیدگی در توزیع نرمال به ویژگی‌های شکل توزیع اشاره دارد و مشخص می‌کند که توزیع چگونه نسبت به توزیع نرمال ایده‌آل انحراف دارد. کشیدگی در واقع به میزان “بلندی” یا “پهنای” دم‌های توزیع اشاره می‌کند و می‌تواند اطلاعات مهمی درباره پراکندگی داده‌ها ارائه دهد.

انواع کشیدگی

1. کشیدگی مثبت: در این حالت، توزیع دارای دم‌های بلندتر در سمت راست میانگین است. داده‌ها بیشتر به سمت چپ متمایل هستند و احتمال وجود مقادیر بزرگ‌تر از میانگین بیشتر می‌باشد. این نوع کشیدگی معمولاً نشان‌دهنده وجود مقادیر پرت یا افراطی در سمت راست است.
2. کشیدگی منفی: در اینجا، توزیع دارای دم‌های بلندتر در سمت چپ میانگین است. داده‌ها بیشتر به سمت راست متمایل هستند و احتمال وجود مقادیر کوچک‌تر از میانگین بیشتر می‌باشد. این نوع کشیدگی معمولاً نشان‌دهنده وجود مقادیر پرت در سمت چپ است.

از دست ندهید: آشنایی با نرم افزار آماری SPSS

اهمیت توزیع نرمال

توزیع نرمال در بسیاری از آزمون‌های آماری به‌عنوان فرض اصلی، مورداستفاده قرار می‌گیرد. برای مثال، آزمون t، آزمون ANOVA و بسیاری از روش‌های تحلیل و رگرسیون به این فرض تکیه می‌کنند که داده‌ها از توزیع نرمال پیروی می‌نمایند. این موضوع باعث می‌شود که در بسیاری از تحلیل‌ها و تفسیرها، توزیع نرمال به‌عنوان یک مدل مرجع موردتوجه قرار گیرد.

توزیع نرمال به دلیل وجود ابزارهای آماری و نرم‌افزارهای تحلیلی متنوع که به‌راحتی می‌توانند با این نوع توزیع کار کنند، به پژوهشگران و تحلیلگران این امکان را می‌دهد تا به‌سرعت به تفسیر و تحلیل داده‌های خود بپردازند. به همین دلیل، شناخت و درک توزیع نرمال یکی از مهارت‌های اساسی برای هر پژوهشگر و تحلیل‌گر داده‌ها به شمار می‌آید.

منحنی توزیع نرمال

این منحنی به طور متقارن حول میانگین توزیع قرار دارد و به شکل زنگی است. ویژگی‌های بارز منحنی توزیع نرمال شامل متقارن بودن آن نسبت به میانگین، وجود دو پارامتر اصلی یعنی میانگین (µ) و انحراف معیار (σ) می‌باشد. میانگین نقطه‌ای است که منحنی در آن به بالاترین ارتفاع می‌رسد و انحراف معیار نشان‌دهنده میزان پراکندگی داده‌ها از میانگین است.

فرمول توزیع نرمال

فرمول توزیع نرمال به شکل ساده به‌صورت زیر است:

f(x)=12πσe−(x−μ)22σ2f(x)=2π

​σ1​e−2σ2(x−μ)2​

در اینجا:

• f(x): چگالی احتمال در نقطه x  را نشان می‌دهد.
• μ: میانگین توزیع است.
• σ: انحراف معیار توزیع است.
• E: عدد نپر تقریباً 2.718 است.
• π: عدد پی تقریباً 3.14159 است.

این فرمول توزیع نرمال را توصیف می‌کند و ویژگی‌های منحنی زنگی آن را نشان می‌دهد.

مقاله پیشنهادی برای شما: الگوریتم فراابتکاری کرم شب‌تاب

جدول توزیع نرمال

جدول توزیع نرمال ابزاری است که برای پیداکردن احتمال‌ها و درصدها در توزیع نرمال استاندارد با میانگین 0 و انحراف معیار 1 استفاده می‌شود. ابتدا باید Z-score را محاسبه کنید که به این صورت است:  Z=(X−μ)σZ=σ(X−μ)​

که در آن:

• X: مقدار موردنظر
• μ: میانگین
• σ: انحراف معیار

مطلب پیشنهادی: پیمایش درخت در ساختمان داده

پارامترهای توزیع نرمال

پارامترهای توزیع نرمال شامل دو مورد اصلی هستند: میانگین و انحراف معیار

1. میانگین

میانگین نشان‌دهنده مرکز توزیع است و مقدار متوسط داده‌ها را مشخص می‌کند. در توزیع نرمال، میانگین، میانه و مد همواره برابر هستند.

2. انحراف معیار

مقادیر بزرگ‌تر انحراف معیار به معنای پراکندگی بیشتر داده‌ها و مقادیر کوچک‌تر به معنای نزدیک‌تر بودن داده‌ها به میانگین است.

نحوه استفاده از توزیع نرمال در امور مالی

توزیع نرمال در امور مالی، کاربردهای مهمی دارد از جمله مواردی که در ادامه اشاره شده است:

• مدل‌سازی بازده‌های سرمایه‌گذاری

بازده‌های سرمایه‌گذاری (مانند سهام) معمولاً در بازه‌های زمانی مختلف (روزانه، هفتگی، ماهانه) به طور پیوسته ثبت می‌شوند. این بازده‌ها توزیع نرمال دارند که به تحلیل‌گران کمک می‌کند تا رفتار تاریخی و پیش‌بینی‌های آینده را مدل‌سازی کنند.

• تحلیل ریسک (Value at Risk – VaR)

با فرض توزیع نرمال بازده‌ها، می‌توان به‌راحتی VaR را محاسبه کرد. این ابزار به سرمایه‌گذاران کمک می‌کند تا حدود ریسک ضررها را در یک افق زمانی مشخص پیش‌بینی کنند.

• مدل‌سازی قیمت‌گذاری گزینه‌ها

در این مدل، فرض می‌شود که تغییرات قیمت دارایی‌های پایه توزیع نرمال دارند. این فرض به تحلیل‌گران اجازه می‌دهد تا قیمت‌های گزینه‌ها را بادقت بیشتری محاسبه کنند.

• تحلیل حساسیت اقتصادی

با استفاده از توزیع نرمال، می‌توان تأثیر تغییرات در پارامترهای اقتصادی (مانند نرخ بهره، تورم) را بر عملکرد دارایی‌ها بررسی نمود. این تحلیل‌ها به تصمیم‌گیری بهتر در مدیریت پرتفوی کمک می‌کنند.

• پیش‌بینی رفتار بازار

تحلیل‌گران می‌توانند از توزیع نرمال برای پیش‌بینی رفتار قیمت‌های بازار در طول زمان استفاده کنند، به‌طوری که نوسانات و روندهای تاریخی را در تصمیم‌گیری‌های سرمایه‌گذاری لحاظ نمایند.

مثالی از توزیع نرمال

برای درک بهتر توزیع نرمال، بیایید یک مثال واقعی از آن در زمینه مالی بررسی کنیم:

مثال: بازده روزانه سهام

فرض کنید شما به تحلیل بازده روزانه یک سهام خاص (مثلاً سهام شرکت الف) پرداخته‌اید. داده‌ها نشان می‌دهند که بازده‌های روزانه این سهام به طور تقریبی توزیع نرمال هستند.

فرضیات

• میانگین بازده1% یعنی در روز، به‌طور متوسط، سهام 0.1% افزایش می‌یابد
• انحراف معیار5% یعنی نوسانات روزانه در حدود 1.5% است

توزیع نرمال

با استفاده از این اطلاعات، می‌توان توزیع نرمال بازده‌های روزانه را به‌صورت زیر توصیف کرد:

• X∼N(μ,σ2)

که در آن حراف معیار و میانگین:

• μ=0.1%
• σ=1.5%

تحلیل:

باتوجه‌به توزیع نرمال، می‌توانیم بگوییم:

• حدود 68% از روزها، بازده‌های سهام در بازه [μ−σ,μ+σ] یعنی [−1.4%,1.6%]خواهد بود.
• حدود 95% از روزها، بازده‌ها در بازه [μ−2σ,μ+2σ] یعنی [−2.9%,3.1%]خواهد بود.

با استفاده توزیع نرمال، سرمایه‌گذاران می‌توانند به‌راحتی ریسک و پتانسیل بازده را تحلیل کنند و تصمیمات بهتری برای سرمایه‌گذاری بگیرند. توزیع نرمال می‌تواند در مدل‌سازی و تحلیل داده‌ های مالی دارای کارایی فراوانی است.

بخوانید: تورم نقطه‌ به‌ نقطه چیست؟

سخن پایانی

توزیع نرمال که به‌عنوان توزیع گاوسی نیز شناخته می‌شود، یکی از مهم‌ترین توزیع‌های آماری است که در بسیاری از زمینه‌ها، از جمله انجام پروژه علوم اجتماعی، طبیعی و مالی، کاربرد دارد. این توزیع به‌صورت یک منحنی زنگی شکل نمایش داده می‌شود. درک صحیح این توزیع و خواص آن به کاربران این امکان را می‌دهد که از آن در زمینه‌های مختلف استفاده کنند و به بینش‌های عمیق‌تری در این حوزه دست یابند.

سوالات پرتکرار

1. منظور از توزیع نرمال چیست؟

توزیع نرمال مدلی است برای توصیف رفتار آماری یک مجموعه‌داده که در آن بیشتر داده‌ها در اطراف میانگین متمرکز شده‌اند و بافاصله گرفتن از میانگین، فراوانی داده‌ها، کاهش می‌یابد.

2. چرا توزیع نرمال“ نرمال“ نامیده می شود؟

توزیع نرمال به دلیل شکل خاص منحنی آن که شبیه به زنگ است (به آن منحنی زنگی نیز گفته می‌شود) و همچنین ویژگی‌های آماری خاصی که دارد، نرمال نامیده می‌شود. دلیل دیگر این نام‌گذاری، اهمیت آن در نظریه حد مرکزی است که نشان می‌دهد تحت شرایطی، توزیع میانگین‌ها به سمت توزیع نرمال، میل می‌کند.

3. محدودیت های توزیع نرمال در امور مالی چیست؟

توزیع نرمال در امور مالی باوجود کاربردهای گسترده، محدودیت‌هایی نیز دارد. یکی از این محدودیت‌ها فرض نرمال بودن بازده‌هاست که در واقعیت ممکن است برقرار نباشد و بازده‌ها تحت‌تأثیر عوامل غیرخطی و بحران‌های مالی قرار گیرند.

4. توزیع نرمال برای چه مواردی استفاده می شود؟

این توزیع برای مدل‌سازی پدیده‌هایی به کار می‌رود که دارای ویژگی‌های تصادفی هستند و در آن‌ها مقادیر به طور طبیعی در اطراف یک میانگین متمرکز شده‌اند؛ مثلاً در اندازه‌گیری‌‌های فیزیکی و همچنین در تحلیل‌های ریسک و خطا در آمار.

5. ویژگی های یک توزیع نرمال چیست؟

در این توزیع، حدود 68 درصد داده‌ها در یک انحراف معیار از میانگین و حدود 95 درصد در دو انحراف معیار قرار دارند. ویژگی محوری این توزیع این است که میانگین، میانه و نما همگی برابرند و همچنین داده‌ها به تدریج از وسط منحنی به سمت دو طرف کاهش می‌یابند.

6. چگونه می دانید که داده ها به طور نرمال توزیع شده اند؟

با استفاده از هیستوگرام یا نمودار جعبه‌ای، می‌توانید شکل توزیع داده‌ها را مشاهده کنید.

7. چگونه از جدول توزیع نرمال استفاده می کنید؟

جدول توزیع نرمال به‌منظور یافتن احتمال وقوع یک متغیر تصادفی نرمال استاندارد (با میانگین صفر و واریانس یک) استفاده می‌شود. ابتدا باید مقدار Z را محاسبه کنیم که نمایانگر موقعیت یک نقطه در توزیع است. سپس با استفاده از جدول، می‌توانیم احتمال مربوط به آن مقدار Z را پیدا کنیم.