الگوریتم کروسکال چیست؟
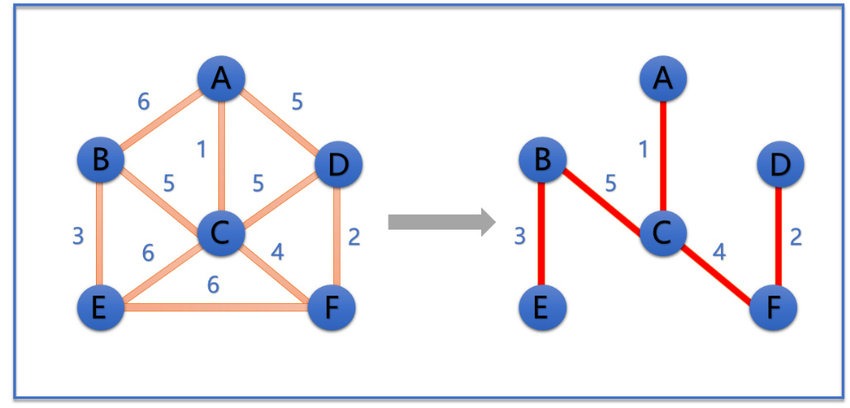
در دنیای پیچیده گرافها، جایی که گرهها و یالها یک شبکه را تشکیل میدهند، پیدا کردن راهی برای پوشش دادن همه گرهها با کمترین هزینه ممکن، یک چالش اساسی است. الگوریتم کروسکال، یکی از قدرتمندترین ابزارها برای حل این مسئله است. این الگوریتم به ما کمک میکند تا در یک گراف وزندار، کمترین درخت پوشا را پیدا کنیم. درخت پوشا، زیرگرافی است که همه گرههای اصلی را شامل میشود و هیچ دورهای ندارد. در این مقاله، به بررسی دقیق کروسکال، کاربردهای آن و پیچیدگی زمانی آن خواهیم پرداخت؛ پس با ما همراه باشید.
کروسکال چیست؟
الگوریتم کروسکال یک الگوریتم حریصانه است که به صورت مرحله به مرحله، یالهایی را به درخت پوشا اضافه میکند. این الگوریتم با مرتبسازی یالها بر اساس وزن آنها شروع میشود. سپس، با انتخاب یال با کمترین وزن، به شرطی که دور ایجاد نکند، درخت پوشا را میسازد. این روند تا زمانی ادامه مییابد که همه گرهها به درخت اضافه شوند.
انجام پروژههای تحلیل داده با بهترین هزینه
مراحل اجرای کروسکال
مراحل اجرای الگوریتم کروسکال، به صورت زیر است:
- مرتبسازی یالها: همه یالهای گراف را بر اساس وزن آنها به صورت صعودی مرتب میکنیم.
- ایجاد مجموعههای مجزا: هر گره را به عنوان یک مجموعه مجزا در نظر میگیریم.
- بررسی یالها: به ترتیب، یالهای مرتب شده را بررسی میکنیم.
- اضافه کردن یال: اگر دو سر یک یال در مجموعههای مجزا قرار داشته باشند، آن یال را به درخت پوشا اضافه میکنیم و دو مجموعه مربوطه را ادغام میکنیم.
- تکرار: مرحله سوم و چهرام را تا زمانی که همه گرهها به یک مجموعه واحد تعلق بگیرند، تکرار میکنیم.
مطلب پیشنهادی: الگوریتم گله اسب چیست؟
پیادهسازی کروسکال
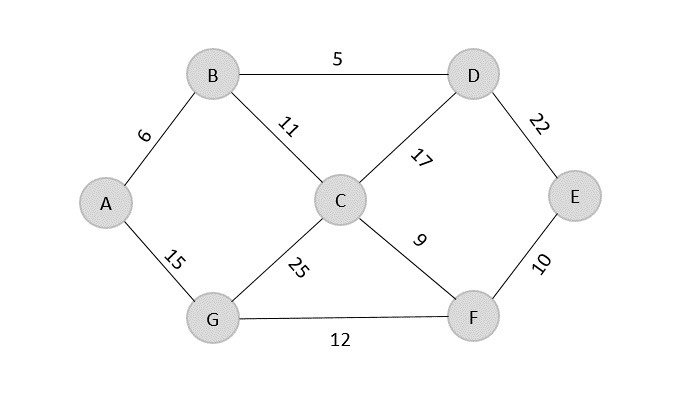
الگوریتم کروسکال را میتوان با استفاده از زبانهای برنامهنویسی مختلف پیادهسازی کرد. برای پیادهسازی این الگوریتم، به یک ساختار داده مناسب برای نمایش گراف و یک ساختار داده برای مدیریت مجموعههای مجزا نیاز داریم. ساختار دادههای رایجی که برای این منظور استفاده میشوند شامل ماتریس مجاورت برای نمایش وزن یالها بین گرهها، لیست مجاورت برای نمایش همسایگان هر گره و ساختار دادهی اتحاد-یافتن برای مدیریت مجموعههای مجزا هستند.
کاربردهای الگوریتم کروسکال
الگوریتم کروسکال، به عنوان یکی از الگوریتمهای پایهای در نظریه گرافها، کاربردهای بسیار گستردهای در حوزههای مختلف دارد. این الگوریتم با پیدا کردن کمترین درخت پوشا در یک گراف وزندار، به ما کمک میکند تا مسائل بهینهسازی مختلفی را حل کنیم. در ادامه، برخی از مهمترین کاربردهای این الگوریتم را به طور مفصل بررسی میکنیم:
طراحی شبکههای ارتباطی
یکی از کاربردهای کروسکال در شبکه های ارتباطی، طراحی شبکههای کامپیوتری است. به این صورت که هر رایانه را به عنوان یک گره و هر اتصال بین دو رایانه را به عنوان یک یال در نظر میگیریم. سپس، با استفاده از این الگوریتم، کمترین درخت پوشا را پیدا میکنیم که نشاندهندهی کمترین هزینه برای اتصال همه رایانهها است. از الگوریتم کروسکال در طراحی شبکههای تلفن هم استفاده تا هزینههای کابلکشی به حداقل برسد.
طراحی مدارهای الکترونیکی
از کاربردهای دیگر این الگوریتم، طراحی مدارهای الکترونیکی مانند طراحی مدارهای مجتمع است. کروسکال میتواند برای یافتن کوتاهترین مسیر بین اجزای مختلف مدار استفاده شود. این کار به کاهش طول سیمها و در نتیجه کاهش تداخل و افزایش سرعت مدار کمک میکند.
برنامهریزی تولید
در مسائل برنامهریزی تولید، میتوان از کروسکال برای تخصیص بهینه منابع استفاده کرد. به عنوان مثال، برای تخصیص ماشینآلات به وظایف مختلف، میتوان هر ماشین را به عنوان یک گره و هر وظیفه را به عنوان یک یال در نظر گرفت و سپس با استفاده از این الگوریتم، کمترین هزینه تخصیص را پیدا کرد.
جغرافیا و نقشه برداری
در مسائل جغرافیایی و نقشه برداری، میتوان از الگوریتم کروسکال برای یافتن کوتاهترین مسیر بین نقاط مختلف استفاده کرد. به عنوان مثال، میتوان از این الگوریتم برای پیدا کردن کوتاهترین مسیر بین شهرها یا نقاط مختلف یک نقشه استفاده کرد.
علوم کامپیوتر
کروسکال به عنوان زیربنای بسیاری از الگوریتمهای جستجو و بهینهسازی در علوم کامپیوتر استفاده میشود. از این الگوریتم همچنین در الگوریتمهای یادگیری ماشین، برای ساختن مدلهای درختی استفاده میشود.
سایر کاربردها
این الگوریتم برای یافتن کمترین هزینه برای اتصال همه مصرفکنندگان به شبکه برق، برای طراحی شبکههای حمل و نقل با کمترین هزینه و برای تحلیل دادههای بیولوژیکی و پیدا کردن روابط بین ژنها هم کاربرد دارد.
به طور خلاصه، کروسکال ابزاری قدرتمند برای حل مسائل بهینهسازی در حوزههای مختلف است. این الگوریتم با پیدا کردن کمترین درخت پوشا در یک گراف وزندار، به ما کمک میکند تا تصمیمات بهتری بگیریم و منابع را بهینه کنیم.
پیچیدگی زمانی کروسکال
پیچیدگی زمانی الگوریتم کروسکال به روش مرتبسازی یالها و ساختار دادهای که برای مدیریت مجموعههای مجزا استفاده میشود، بستگی دارد. اگر از الگوریتم مرتبسازی سریع برای مرتبسازی یالها و ساختار دادهی اتحاد-یافتن برای مدیریت مجموعههای مجزا استفاده کنیم، پیچیدگی زمانی کروسکال برابر با O(E log V) خواهد بود، که در آن E تعداد یالها و V تعداد گرههای گراف است.
مطلب پیشنهادی: الگوریتم بهینه سازی فاخته چیست؟
مثالی از اجرای کروسکال روی یک گراف خاص
فرض کنید گرافی با ۶ گره و ۹ یال به شرح زیر داریم:
| راس مبدا | راس مقصد | وزن |
| 0 | 1 | 4 |
| 0 | 2 | 3 |
| 1 | 2 | 1 |
| 1 | 3 | 2 |
| 2 | 3 | 4 |
| 3 | 4 | 2 |
| 4 | 5 | 4 |
| 5 | 0 | 7 |
| 4 | 0 | 6 |
میتوانیم از الگوریتم کروسکال برای پیدا کردن کمترین درخت پوشای این گراف استفاده کنیم.
برای اجرای این الگوریتم، باید روشهای زیر را استفاده کنیم:
- مرتبسازی یالها بر اساس وزن:
ابتدا یالها را بر اساس وزن آنها به صورت صعودی مرتب میکنیم. نتیجهی این مرحله به صورت زیر است:
| راس مبدا | راس مقصد | وزن |
| 1 | 2 | 1 |
| 1 | 3 | 2 |
| 3 | 4 | 2 |
| 0 | 2 | 3 |
| 2 | 3 | 4 |
| 4 | 5 | 4 |
| 0 | 1 | 4 |
| 4 | 0 | 6 |
| 5 | 0 | 7 |
- ایجاد مجموعههای مجزا:
برای هر گره یک مجموعه جداگانه در نظر میگیریم. در این مثال، ۶ مجموعه مجزا خواهیم داشت که هر مجموعه شامل یک راس است.
- بررسی یالها به ترتیب وزن:
به ترتیب یالها را از کمترین وزن بررسی میکنیم. در صورتی که اضافه کردن یال باعث ایجاد دور نشود، آن را به درخت پوشا اضافه میکنیم و دو مجموعه مربوط به آن یال را ادغام میکنیم.
- بررسی یال (۱, ۲) با وزن ۱:
اضافه کردن این یال باعث ایجاد دور نمیشود، بنابراین آن را به درخت پوشا اضافه میکنیم و مجموعههای مربوط به راسهای ۱ و ۲ را ادغام میکنیم.
- بررسی یال (۱, ۳) با وزن ۲:
اضافه کردن این یال باعث ایجاد دور نمیشود، بنابراین آن را به درخت پوشا اضافه میکنیم و مجموعههای مربوط به راسهای ۱ و ۳ را ادغام میکنیم (که قبلا با راس ۲ ادغام شده بود).
- بررسی یال (۳, ۴) با وزن ۲:
اضافه کردن این یال باعث ایجاد دور نمیشود، بنابراین آن را به درخت پوشا اضافه میکنیم و مجموعههای مربوط به راسهای ۳ و ۴ را ادغام میکنیم.
- بررسی یال (۰, ۲) با وزن ۳:
اضافه کردن این یال باعث ایجاد دور نمیشود، بنابراین آن را به درخت پوشا اضافه میکنیم و مجموعههای مربوط به راسهای ۰ و ۲ را ادغام میکنیم.
- بررسی یال (۰, ۱) با وزن ۴:
از آنجایی که راسهای ۰ و ۱ قبلا در یک مجموعه قرار دارند، اضافه کردن این یال باعث ایجاد دور میشود، بنابراین آن را به درخت پوشا اضافه نمیکنیم.
- بررسی یالهای (۲, ۳) و (۴, ۵) با وزن ۴:
به دلیل اینکه راسهای ۲ و ۳ و همچنین ۴ و ۵ قبلا در یک مجموعه قرار دارند، اضافه کردن این یالها باعث ایجاد دور میشود، بنابراین آنها را به درخت پوشا اضافه نمیکنیم.
به همین ترتیب، برای یالهای (۴, ۰) و (۵, ۰) نیز همین استدلال را میتوان تکرار کرد.
- درخت پوشا:
در نهایت، درخت پوشای این گراف شامل یالهای زیر میشود:
| راس مبدا | راس مقصد | وزن |
| 1 | 2 | 1 |
| 1 | 3 | 2 |
| 3 | 4 | 2 |
| 0 | 2 | 3 |
| 0 | 1 | 4 |
همانطور که مشاهده میشود، این درخت پوشا تمام گرههای گراف را شامل شده و هیچ دور ندارد. همچنین، مجموع وزن یالهای آن کمترین مقدار ممکن است.
خروجی کد:
درخت پوشا:
Python
(1, 2) – وزن: 1
(1, 3) – وزن: 2
(3, 4) – وزن: 2
(0, 2) – وزن: 3
مطلب پیشنهادی: الگوریتم علی بابا و چهل دزد
تفاوت بین الگوریتم پریم و کروسکال
الگوریتم کروسکال و پریم هر دو برای یافتن درخت پوشای کمینه (MST) در یک گراف وزندار استفاده میشوند. هر دو الگوریتم به صورت حریصانه عمل میکنند، اما رویکرد آنها برای ساختن درخت پوشا متفاوت است.
کروسکال با یالها شروع میکند. ابتدا تمام یالها را بر اساس وزن به صورت صعودی مرتب میکند و پس از آن به ترتیب یالها را بررسی میکند. اگر اضافه کردن یک یال به درخت پوشا در حال ساخت دوری ایجاد نکند، آن یال را به درخت اضافه میکند.
الگوریتم پریم با یک راس شروع میکند و به صورت تدریجی به درخت پوشا اضافه میکند. در هر مرحله، نزدیکترین راس به درخت حاضر را انتخاب کرده و آن را به درخت اضافه میکند.
تفاوتهای کلیدی دو الگوریتم
- شروع الگوریتم: کروسکال با یالها شروع میکند، در حالی که پریم با یک راس.
- نحوه ساخت درخت: کروسکال یالها را به صورت مستقل بررسی میکند و آنها را به درخت اضافه میکند، در حالی که پریم به صورت تدریجی درخت را گسترش میدهد.
- پیچیدگی زمانی: پیچیدگی زمانی هر دو الگوریتم به پیادهسازی و ساختار دادههای استفاده شده بستگی دارد، اما به طور کلی، هر دو الگوریتم پیچیدگی زمانی O(E log V) دارند که در آن E تعداد یالها و V تعداد رئوس گراف است.
| مشخصه | کروسکال | پریم |
| شروع | با یالها | با یک راس |
| ساخت درخت | یال به یال | به صورت تدریجی |
| ساختار داده | اتحاد یافتن | اولویتبندی |
| پیچیدگی زمانی | O (E log V) | O (E log V) |
چه زمانی از کدام الگوریتم استفاده کنیم؟
انتخاب بین الگوریتم کروسکال و پریم به عوامل مختلفی از جمله ساختار گراف، پیادهسازی و منابع موجود بستگی دارد. به صورت کل کروسکال برای گرافهایی با یالهای کم و رئوس زیاد مناسبتر است و پریم برای گرافهایی با رئوس کم و یالهای زیاد مناسبتر است.
مطلب پیشنهادی: هوش تجاری چیست؟
جمعبندی
الگوریتم کروسکال یک الگوریتم قدرتمند و کارآمد برای پیدا کردن کمترین درخت پوشا در یک گراف وزندار است. این الگوریتم در بسیاری از زمینههای مختلف کاربرد دارد و به عنوان یکی از الگوریتمهای اساسی در نظریه گرافها شناخته میشود. با درک عمیق از کروسکال و کاربردهای آن، میتوانیم در حل بسیاری از مسائل پیچیده در حوزههای مختلف آن را استفاده کنیم. هر دو الگوریتم پریم و کروسکال برای یافتن درخت پوشای کمینه استفاده میشوند و هر کدام مزایا و معایب خاص خود را دارند. انتخاب الگوریتم مناسب به شرایط مسئله و ترجیحات برنامهنویس بستگی دارد.





.svg)
