الگوریتم دایجسترا چیست؟ آشنایی با گراف ها با مثال

الگوریتم‌ها نقش بسیار مهمی در علم کامپیوتر ایفا می‌کنند و اساس بسیاری از فرآیندهای محاسباتی و تکنولوژی‌های مدرن هستند. اگر الگوریتم‌ها اختراع نشده بودند، علم کامپیوتر در مرحله فعلی نبود. دنیایی از الگوریتم‌ها مختلف وجود دارد. از الگوریتم گله اسب و الگوریتم میگو گرفته تا الگوریتم فرا ابتکاری. در این بین یک الگوریتم مهم وجود دارد، الگوریتم داجسترا. الگوریتم دایجسترا (Dijkstra)، یکی از معروف‌ترین و کاربردی‌ترین الگوریتم‌ها در علم کامپیوتر است که برای یافتن کوتاه‌ترین مسیر از یک راس به سایر رئوس در یک گراف وزن‌دار غیر منفی استفاده می‌شود. الگوریتم دایجسترا به افتخار مخترع آن، ادموند دایجسترا، نامگذاری شده است. ادموند دایجسترا، یک دانشمند کامپیوتر هلندی بود که به دلیل کارهای ارزشمندش در زمینه الگوریتم‌ها و نظریه گراف‌ها شناخته می‌شود. ما در این مقاله قصد داریم تا الگوریتم دایجسترا را به صورت کامل بررسی کنیم و با مزایا و کاربردهای آن آشنا شویم.

تاریخچه الگوریتم دایجسترا

الگوریتم دایجسترا اولین بار در سال 1956 توسط ادموند دایجسترا معرفی شد و در سال 1959 در مقاله‌ای با عنوان “یادداشتی در مورد دو مسأله در ارتباط با گراف‌ها” منتشر شد. این الگوریتم به سرعت محبوبیت پیدا کرد و به یکی از ابزارهای اساسی در حل مسائل کوتاه‌ترین مسیر تبدیل شد.

الگوریتم دایجسترا در گراف

الگوریتم دایجسترا یکی از الگوریتم‌های مهم و پرکاربرد در نظریه گراف است که برای یافتن کوتاه‌ترین مسیر از یک رأس مبدأ به تمامی رئوس دیگر در یک گراف وزن‌دار استفاده می‌شود. این الگوریتم به دلیل ویژگی‌های منحصر به فرد و کارایی بالا، در بسیاری از مسائل و کاربردهای واقعی به کار گرفته می‌شود. الگوریتم دایجسترا به عنوان یک الگوریتم حریصانه شناخته می‌شود و فقط بر روی گراف‌هایی که وزن لبه‌های آنها مثبت است، قابل اجراست.

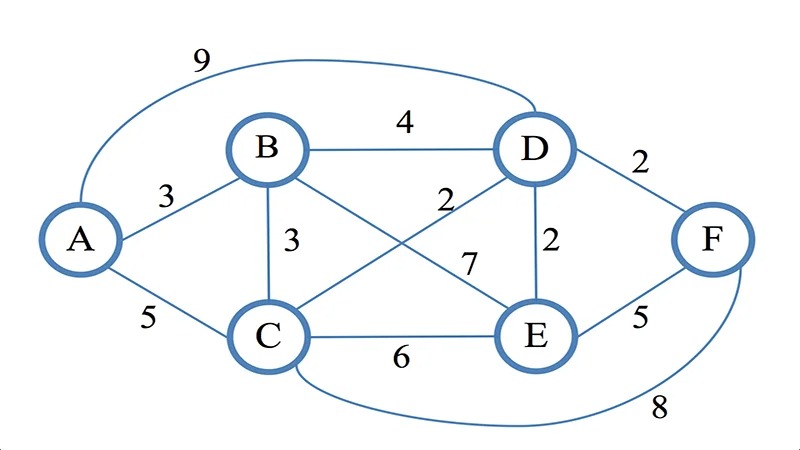
انواع گراف‌ها

برای درک بهتر الگوریتم دایجسترا نیاز است تا با گراف‌ها بیشتر آشنا شویم. گراف‌ها به دو دسته کلی گراف‌های جهت‌دار و بدون جهت تقسیم می‌شوند که هر کدام ویژگی‌ها و کاربردهای خاص خود را دارند.

گراف بدون جهت

گراف‌های بدون جهت دارای لبه‌هایی هستند که جهت مشخصی ندارند و به عبارتی، حرکت در هر دو جهت امکان‌پذیر است. این نوع گراف‌ها معمولاً برای نمایش روابط دوطرفه استفاده می‌شوند، مانند دوستی‌ها در شبکه‌های اجتماعی یا اتصالات در شبکه‌های تلفنی.

گراف جهت‌دار

در مقابل، گراف‌های جهت‌دار دارای لبه‌هایی با جهت مشخص هستند که نشان‌دهنده روابط یک‌طرفه می‌باشند. این گراف‌ها معمولاً در مواردی به کار می‌روند که ترتیب و جهت ارتباط‌ها مهم است، مانند شبکه‌های جریان کار، نمودارهای وابستگی و شبکه‌های جاده‌ای یک‌طرفه.

گراف وزنی

یک گراف زمانی وزنی نامیده می‌شود که هر لبه آن دارای یک وزن مشخص باشد. این وزن می‌تواند نشان‌دهنده فاصله، زمان یا هر معیار دیگری باشد که برای مدل‌سازی ارتباط بین جفت رئوس استفاده می‌شود. به عنوان مثال، در یک نقشه راه‌ها، وزن‌ها می‌توانند نشان‌دهنده فاصله‌های بین شهرها باشند یا در یک شبکه کامپیوتری، وزن‌ها ممکن است نشان‌دهنده زمان تأخیر در ارتباط بین گره‌ها باشند.

انجام پروژه پایتون

مبانی اصلی الگوریتم دایجسترا

الگوریتم دایجسترا یکی از مهم‌ترین و پرکاربردترین الگوریتم‌ها در علوم کامپیوتر و مهندسی برای پیدا کردن کوتاه‌ترین مسیر در یک گراف وزن‌دار است. این الگوریتم در موارد متعددی از جمله مسیریابی شبکه، برنامه‌ریزی ترافیک، و حل مسائل مرتبط با نقشه‌ها و سیستم‌های اطلاعات جغرافیایی کاربرد دارد. در اینجا، اصول و مفاهیم اساسی این الگوریتم را با جزئیات بیشتری مورد بررسی قرار می‌دهیم:

نقطه شروع الگوریتم دایجسترا

الگوریتم دایجسترا از یک گره خاص، که به آن گره مبدأ می‌گوییم، شروع به کار می‌کند. هدف این الگوریتم یافتن کوتاه‌ترین مسیر از گره مبدأ به تمام گره‌های دیگر در گراف است. این فرایند شامل ارزیابی مسیرهای ممکن و به‌روزرسانی مداوم اطلاعات مربوط به کوتاه‌ترین مسیرها است.

ثبت و به‌روزرسانی مسیرهای کوتاه

در حین اجرای الگوریتم دایجسترا، سوابق کوتاه‌ترین مسیر شناخته‌شده از گره مبدأ به هر گره دیگر ثبت می‌شود. هرگاه الگوریتم مسیری کوتاه‌تر از مسیر قبلی پیدا کند، این سوابق به‌روز می‌شوند. این کار تا زمانی ادامه پیدا می‌کند که تمامی مسیرهای ممکن بررسی شده و به‌روز رسانی‌ها انجام شده باشد.

علامت‌گذاری گره‌های بازدید شده

پس از پیدا کردن کوتاه‌ترین مسیر به یک گره، آن گره به‌عنوان گره بازدید شده علامت‌گذاری می‌شود. این علامت‌گذاری به الگوریتم دایجسترا کمک می‌کند تا بداند کدام گره‌ها نیاز به بررسی مجدد ندارند و می‌تواند تمرکز خود را بر روی گره‌های دیگر قرار دهد.

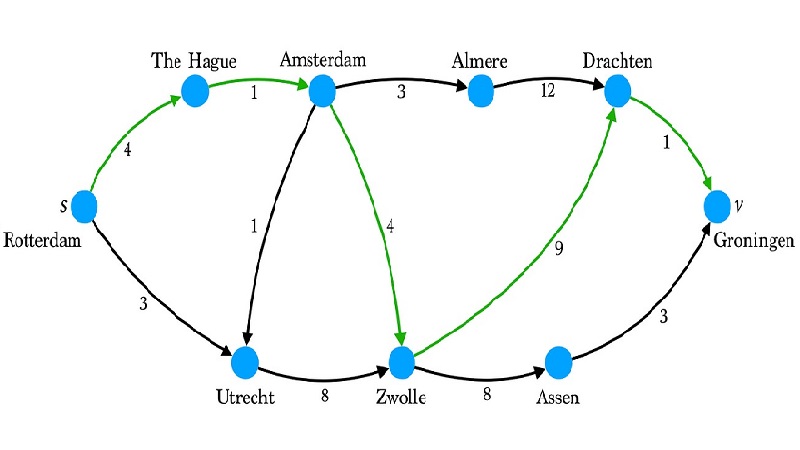
کاربردهای الگوریتم دایجسترا

الگوریتم دایجسترا، یکی از مهم‌ترین الگوریتم‌ها در حوزه نظریه گراف و علم کامپیوتر است که برای پیدا کردن کوتاه‌ترین مسیر بین دو نقطه در یک گراف وزن‌دار مورد استفاده قرار می‌گیرد. این الگوریتم، با توجه به دقت و کارایی بالای خود، در زمینه‌های مختلفی کاربرد دارد.

در ادامه، به بررسی جامع کاربردها و مزایای الگوریتم دایجسترا در صنایع و حوزه‌های مختلف خواهیم پرداخت.

شبکه‌های ارتباطی

یکی از مهم‌ترین کاربردهای الگوریتم دایجسترا در شبکه‌های ارتباطی است. در این حوزه، این الگوریتم برای یافتن کوتاه‌ترین مسیر بین دو نقطه در شبکه‌های کامپیوتری و اینترنت به کار می‌رود. به عنوان مثال:

• مسیریابی در شبکه‌های کامپیوتری: در شبکه‌های گسترده مانند اینترنت، تعیین مسیر بهینه برای ارسال داده‌ها اهمیت بالایی دارد. الگوریتم دایجسترا می‌تواند بهترین مسیر را از یک نقطه به نقطه دیگر با کمترین تاخیر یا هزینه پیدا کند.
• شبکه‌های محلی (LAN): در شبکه‌های محلی نیز از این الگوریتم برای بهبود عملکرد مسیریابی و کاهش زمان تأخیر استفاده می‌شود.

انجام پروژه شبکه و نتورک

نقشه‌برداری و سیستم‌های ناوبری

الگوریتم دایجسترا نقش حیاتی در نقشه‌برداری و سیستم‌های ناوبری دارد. این الگوریتم می‌تواند برای تعیین کوتاه‌ترین مسیر بین دو مکان در سیستم‌های GPS و نقشه‌های دیجیتال مورد استفاده قرار گیرد. برخی از کاربردهای خاص عبارتند از:

• سیستم‌های ناوبری خودروها: استفاده از الگوریتم دایجسترا در سیستم‌های ناوبری خودروها برای ارائه مسیرهای بهینه و کاهش زمان سفر.
• نقشه‌های دیجیتال: به کارگیری این الگوریتم در نقشه‌های دیجیتال و توپوگرافی‌ برای پیشنهاد مسیرهای سریع‌تر و بهینه‌تر به کاربران.

مسائل حمل و نقل و تدارکات

الگوریتم دایجسترا می‌تواند در بهینه‌سازی مسیرهای حمل و نقل و توزیع کالاها نیز بسیار مؤثر باشد. در این زمینه، از الگوریتم دایجسترا برای حل مسائل پیچیده و بهبود کارایی سیستم‌های لجستیکی استفاده می‌شود:

• مدیریت زنجیره تأمین: یافتن مسیرهای بهینه برای توزیع کالاها و کاهش هزینه‌های حمل و نقل.
• حمل و نقل شهری: استفاده از الگوریتم دایجسترا برای بهینه‌سازی مسیرهای حمل و نقل عمومی و کاهش زمان انتظار مسافران.

بازی‌های ویدئویی

الگوریتم دایجسترا در طراحی و توسعه بازی‌های ویدئویی نیز کاربردهای فراوانی دارد. این الگوریتم می‌تواند برای تعیین مسیر حرکت شخصیت‌ها در بازی‌ها مورد استفاده قرار گیرد:

• هوش مصنوعی در بازی‌ها: استفاده از الگوریتم دایجسترا برای تعیین مسیرهای بهینه و ایجاد تجربه بازی بهتر برای کاربران.
• طراحی مراحل بازی: به کارگیری این الگوریتم در طراحی مراحل بازی‌ها برای ایجاد چالش‌های منطقی و جذاب.

سفارش طراحی و ساخت بازی

دیگر کاربردهای الگوریتم دایجسترا

علاوه بر کاربردهای فوق، الگوریتم دایجسترا در زمینه‌های دیگری نیز مورد استفاده قرار می‌گیرد:

• شبکه‌های حمل و نقل: به کارگیری این الگوریتم در بهینه‌سازی شبکه‌های حمل و نقل ریلی و جاده‌ای.
• تحلیل شبکه‌های اجتماعی: استفاده از الگوریتم دایجسترا برای تحلیل و بازاریابی شبکه‌های اجتماعی.

مزایای الگوریتم دایجسترا

الگوریتم دایجسترا به دلیل ویژگی‌های خاص خود، مزایای فراوانی دارد که در ادامه به برخی از مهم‌ترین آن‌ها اشاره خواهیم کرد:

دقت بالا

الگوریتم دایجسترا، به دلیل استفاده از ساختارهای داده مناسب و روش‌های دقیق، توانایی پیدا کردن مسیرهای بهینه را با دقت بالا دارد. این ویژگی باعث می‌شود که در کاربردهایی که نیاز به دقت بالا دارند، بسیار مؤثر باشد.

قابلیت تطبیق با مسائل مختلف

یکی دیگر از مزایای این الگوریتم، قابلیت تطبیق آن با مسائل و نیازهای مختلف است. الگوریتم دایجسترا می‌تواند به راحتی با تغییرات جزئی در ساختار گراف و وزن‌ها تطبیق پیدا کند و همچنان عملکرد بهینه خود را حفظ کند.

سهولت پیاده‌سازی

الگوریتم دایجسترا به دلیل سادگی مفهومی و روش‌های پیاده‌سازی آسان، به راحتی قابل فهم و استفاده است. این ویژگی باعث شده است که این الگوریتم در بسیاری از نرم‌افزارها و سیستم‌های کاربردی پیاده‌سازی شود.

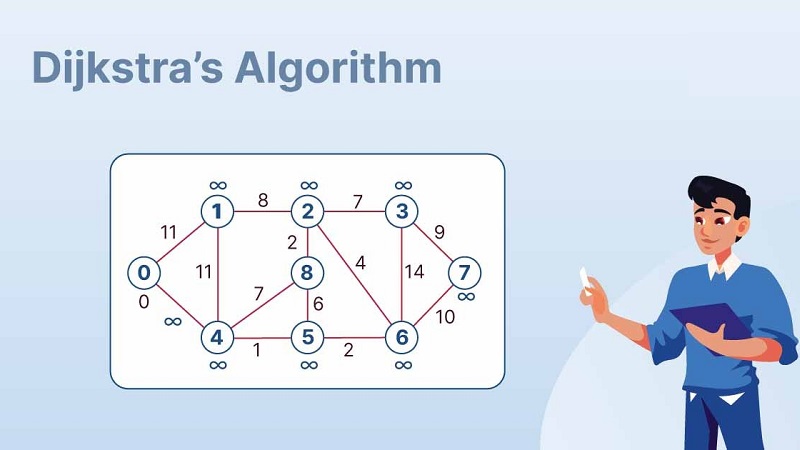
نحوه کار الگوریتم دایجسترا

الگوریتم دایجسترا از یک رویکرد حریصانه (Greedy) برای پیدا کردن کوتاه‌ترین مسیر استفاده می‌کند. این الگوریتم با استفاده از یک مجموعه از راس‌ها که فاصله آن‌ها از راس مبدا مشخص شده است، کار می‌کند و به تدریج راس‌هایی که کوتاه‌ترین مسیر به آن‌ها پیدا شده است را به مجموعه نهایی اضافه می‌کند.

برای درک بهتر نحوه کارکرد الگوریتم دایجسترا، مراحل زیر را با جزئیات بیشتری بررسی می‌کنیم:

مقداردهی اولیه

در آغاز کار، الگوریتم دایجسترا، به هر گره یک مقدار اولیه نسبت داده می‌شود که نمایانگر فاصله تخمینی از گره مبدأ است. این مقدار برای گره مبدأ صفر و برای سایر گره‌ها بی‌نهایت فرض می‌شود. همچنین، مجموعه‌ای از گره‌ها که نیاز به بررسی دارند، تشکیل می‌شود که در ابتدا شامل تمامی گره‌ها است.

انتخاب گره با کمترین فاصله

در هر مرحله، گره‌ای که کمترین فاصله را از گره مبدأ دارد و هنوز بازدید نشده است، انتخاب می‌شود. این گره به‌عنوان گره فعلی در نظر گرفته می‌شود.

به‌روزرسانی فاصله‌ها

برای هر گره همسایه گره فعلی، فاصله جدیدی محاسبه می‌شود که برابر است با مجموع فاصله گره فعلی تا گره مبدأ و وزن یال بین گره فعلی و گره همسایه. اگر این فاصله جدید کمتر از فاصله قبلی ثبت‌شده برای آن گره باشد، فاصله جدید جایگزین می‌شود و مسیر به‌روز می‌گردد.

علامت‌گذاری گره به‌عنوان بازدید شده

پس از بررسی تمامی گره‌های همسایه، گره فعلی به‌عنوان بازدید شده علامت‌گذاری می‌شود و از مجموعه گره‌های نیازمند بررسی حذف می‌شود.

تکرار مراحل

این فرآیند تکرار می‌شود تا زمانی که تمامی گره‌ها بازدید شده و کوتاه‌ترین مسیرها به‌روزرسانی شده باشند.

کسب درآمد از خانه با پروژه‌های کارلنسر

بهینه‌سازی‌ها و کاربردهای پیشرفته

الگوریتم دایجسترا می‌تواند با تغییرات و بهینه‌سازی‌هایی همراه شود که عملکرد آن را در شرایط خاص بهبود بخشد. برخی از این بهینه‌سازی‌ها عبارتند از:

استفاده از ساختار داده‌های بهینه‌تر

با استفاده از ساختار داده‌های پیشرفته مانند فیبوناچی هیپ، می‌توان زمان اجرای الگوریتم را بهبود داد.

پیش‌پردازش گراف

در برخی موارد، می‌توان با انجام پیش‌پردازش‌هایی بر روی گراف، زمان اجرای الگوریتم را کاهش داد.

استفاده در گراف‌های پویا

در گراف‌هایی که به مرور زمان تغییر می‌کنند، می‌توان الگوریتم دایجسترا را با تغییرات کوچکی تطبیق داد تا نیاز به اجرای مجدد کامل الگوریتم نباشد.

مقایسه با سایر الگوریتم‌ها

الگوریتم دایجسترا تنها الگوریتم موجود برای یافتن کوتاه‌ترین مسیرها نیست و الگوریتم‌های دیگری نیز وجود دارند که بسته به شرایط، ممکن است مناسب‌تر باشند. به عنوان مثال:

الگوریتم بلمن-فورد

الگوریتم بلمن-فورد قادر است کوتاه‌ترین مسیرها را در گراف‌هایی که وزن‌های منفی دارند نیز پیدا کند.

الگوریتم فلوید-وارشال

الگوریتم فلوید-وارشال برای یافتن کوتاه‌ترین مسیرها بین تمامی جفت رئوس در گراف به کار می‌رود.

الگوریتم A*

این الگوریتم یک الگوریتم حریصانه و مبتنی بر جستجوی آگاهانه است که برای یافتن کوتاه‌ترین مسیر در گراف‌های با وزن‌های مثبت و منفی کاربرد دارد.

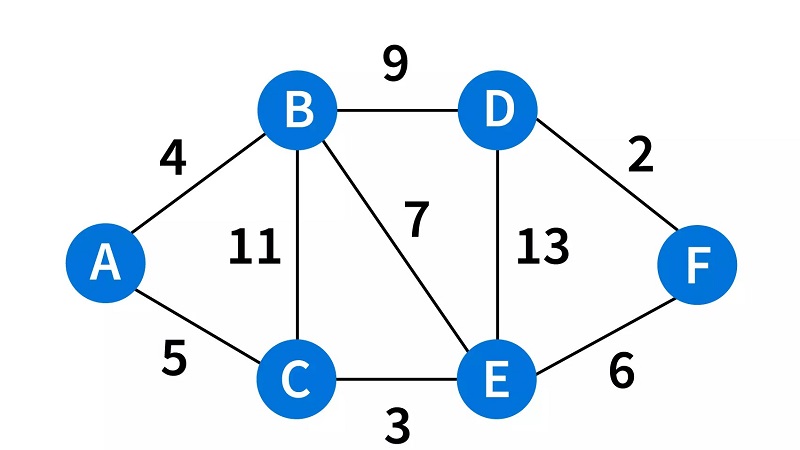
جمع بندی

الگوریتم دایجسترا یکی از مهم‌ترین و پرکاربردترین الگوریتم‌ها در علوم کامپیوتر و مهندسی است که برای یافتن کوتاه‌ترین مسیر بین دو نقطه در یک گراف استفاده می‌شود. الگوریتم دایجسترا به دلیل کارایی بالا، سادگی در پیاده‌سازی، انعطاف‌پذیری و قابلیت بهینه‌سازی، در بسیاری از صنایع و زمینه‌های مختلف کاربرد دارد.